
Some mathematics problems on this site are steeped in history. This one however, had a distinctly modern story. Of course it stems from ideas from a long time ago, but as recently as 1955, it was Louis J.Mordell who posed that it was very difficult to find a new solution for 3. From there it piqued interest from various computer scientist mathematicians and more answers began to be found.
Most recently Numberphile featured a video about how there was no solution for 42 or 74, but this inspired viewers and answers were found for both of these and finally a new answer for 3. These have all been documented by Numberphile on YouTube and helped continue to popularise the problem. As with the Collatz conjecture and the Goldbach conjecture, parts of this problem remain unsolved and is one of the most famous unsolved problems that exist today.
There is some great learning to be had from this, firstly we consider the problem simplified. If I take three integers, cube each one, then sum the total, what numbers can I make? Can I make all numbers? Are there more than one solution for each number?
So what maths is covered? Firstly cube numbers, secondly, what an integer is, thirdly, and perfect for when teaching operations with negative numbers, a negative number cubed will result in a negative. From there we get bucket loads of practice on multiplication and adding with negative numbers.
There is a pattern to the numbers that can’t be obtained by adding three cubes, although the rule isn’t obvious (9 mod 4/5, or numbers that when you divide by 9 you get a remainder of 4 or 5).
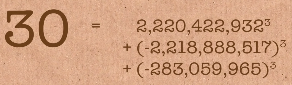
This is not one for spending a lot of time on though – because finding the answer to say 30, is ridiculous.
What is fun is to link this to a spreadsheet or even better – a computer programme. But if you can’t do that – simply challenge students to come up with as many under 500 as they can, similar to other problems like the Goldbach Conjecture.
My Experience
After playing around with what cube numbers are and what they represent. I ask a question. Hmmm…
if we add two cube numbers together, what numbers can we make?
1 + 0 makes 1
1 + 1 makes 2
1 + 2 makes 9
2 + 2 makes 16
oh… we’ve skipped quite a lot there! Maybe we should try adding three cubes together – that might give use some more options…
I then share with them the famous problem and that many mathematicians also asked the same thing, can we find every number as a sum of three cubed integers?
Wait what are integers? Can we define integers? Is zero an integer? Yes. are negative numbers integers? Yes! Are decimals or fraction? Nope sorry, thats not an integer.
Does having zero help! Well yes because we can get 2 and 1 easily by doing what we did at the start but having the third one as 0 cubed.
But do negatives help – try multiplying a negative three times – what happens? How can that help us?
Challenge – have a go at calculating some cubed numbers (positive or negative) and then find combinations of them that sum to make a number less than say 200. How many can we find in five/ten minutes.
This gives me time to check everyone understands what cube numbers are and how to multiply and add with negative numbers.
After a while we see how we did – and then I chat about how some numbers are in fact impossible (see above). It is great for students to see that sometimes there is no answer to a problem in mathematics. I then talk about how the answer for 33, 74 and 42 were only found recently (in the last few years) and that even new answers for numbers like 3 and 7 would be enough to be congratulated in the world of mathematics.
This is usually a great 40 minute activity that I may finish with a cube number challenge using Blooket or gimkit – alternatively with older students – I challenge them to use a computer to help them find an answer they can play around with a spreadsheet or try using Python.
