Paper Based Strategy Games

Low Entry and Rich games to use in the Classroom

One of my favourite resources for students who finish their work earlier, or an extra maths lesson with no planning prepared, is to throw in a pencil and paper strategy game. I also use it as part of competitions when running a competitive maths competition.

Some of these (and often the best) games are often called finite games, which means it will end and there will be a victor (or tie). As part of the strategy, there is often an effect on who goes first or second, and if you add an extra player in to some of these games it creates another level of difficulty and intrigue.

The Grid

I am not sure where I saw this originally, but the premise is simple. Force your opponent to end up in the top right square.

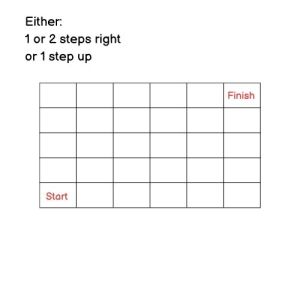
The wonderful thing about this game, is that you can vary the size of the grid, or the moves you can make, and see if it changes the strategy of the game. It is essentially a Nim style game, but with added complexity of your own choosing.

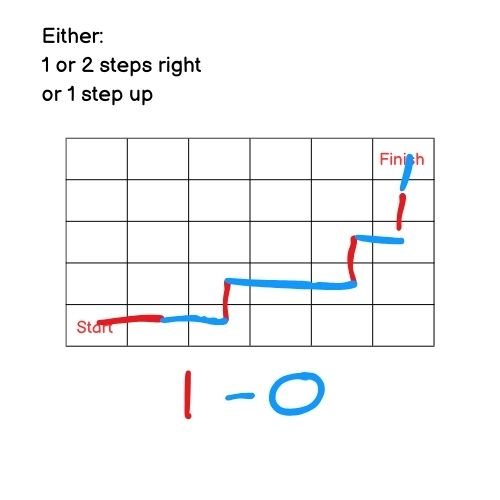
Sprouts

A great game to bring our in the festive period, this has been investigated mathematically to a great detail. The object of the game is to stop your opponent making a move. A move is drawing a line between two sprouts. Essentialy each sprout can have, at most, three lines emerging from it. lines cannot cross other lines, and when you connect two sprouts, you create a new sprout in the middle of your line.

You can choose to start with two three or four sprouts, each one having a different impact on who should go first or second and what strategy to undertake. There is also a different version Brussel Sprouts, where each sprout is a cross + and therefore can have four lines it can connect to rather thatn three.

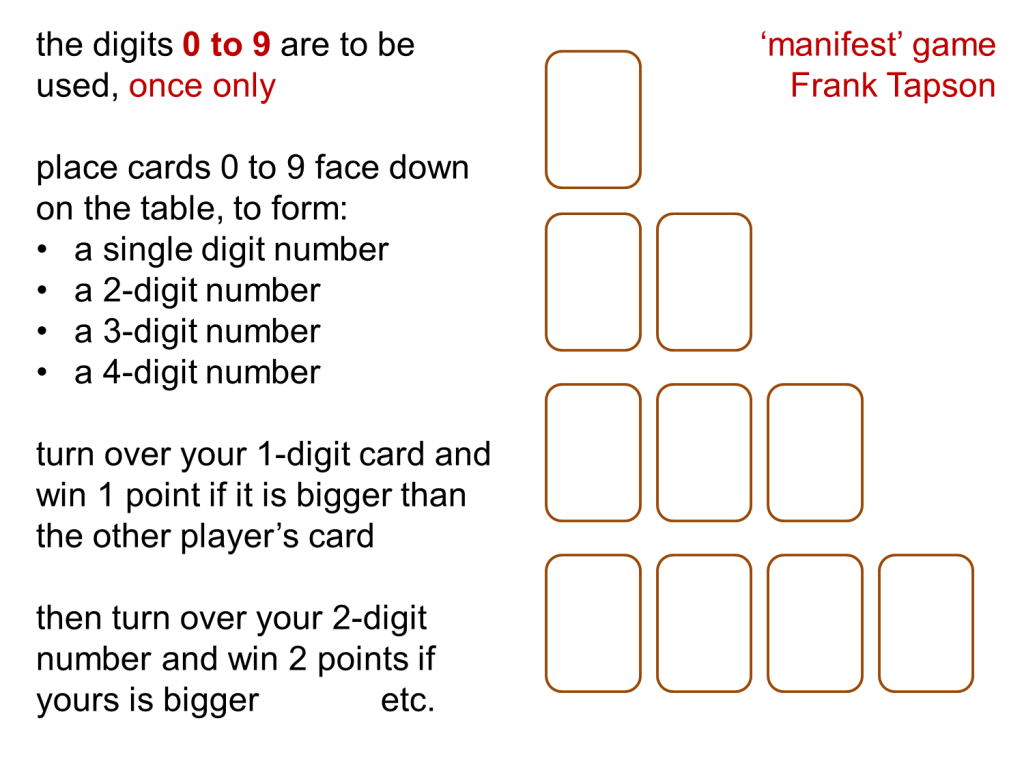
Manifest

I was introduced to this game from the great Don Steward, though credit goes to Frank Tapson. The premise is simple.

Using the digits 0-9 only once, create a 4-digit, 3-digit, 2-digit and 1 digit number. Keep your numbers hidden from your opponent. Then reveal your numbers. You score 4 points if your 4 digit number is bigger, 3 if your 3 digit number is bigger, 2 for your 2 digit and 1 point if your single digit number is bigger.

This is a great lesson into game theory, because you are not necessarily thinking about the best strategy (though there are some key ideas) but thinking about what your opponent is going to do. Essentially you can afford to lose your 4-digit number battle as long as you win the other three, but is your opponent thinking the same thing?

Aggression

I came across this game by Ellie Dix on the Dark Imp website. A game that appeals to my students for its premise – destroying other people’s land and waging war, albeit with numbers.

Basically get creative with a map of differing connected boxes – the size does not matter, but at least sixteen to twenty boxes will do.

Each player takes turns to place their 100 strong army in certain territories. The total you can place is 100, so you have to strategise on where and how many you place. Then once all armies have been placed. Player one can choose to invade a territory next to one with their own army in. So if for example Player one had placed 23 of her army in box G, she could choose to invade any of H B L C or F, if the number is smaller than 23, then that area is captured and Player one crosses the territory in their own colour. They keep their original army, no deductions are made.

The winner is the person with the most territories claimed when neither player can make any more moves.

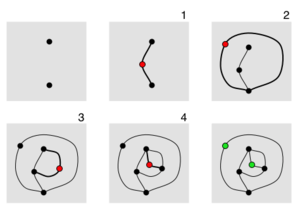
Black Hole

This one is part of the prolific work of Walter Joris, and is called black hole, because at the end of filling in the board, there will be one circle left and all circles touching that one get deleted. The wonderful Ben Orlin from math with bad drawings has the details in his blog that I can’t really do a better job of explaining.

Essentially though, from a pyramid of 21 circles, each player takes turns to fill in a number, in ascending order, so 1, then 2 and then 3. Both place their own 1, and their own 2 etc etc. So that the end of the grid looks like this:

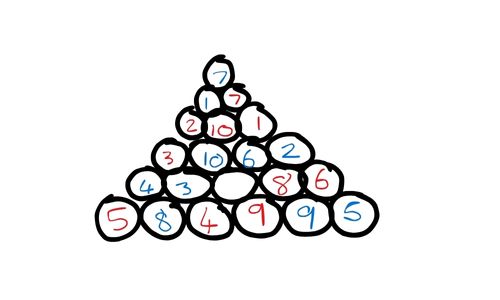
Then all the circles around the blank one are “destroyed”. The winner is the player with the most remaining points. This game can be extended with more circles, providing that you still have an odd number of circles. Or even have more black holes, and perhaps the game ends when you have filled in all your numbers from 1-12 perhaps.

There are loads more mathematical paper games – but these are the ones I use most in class, as well as ultimate tic tac toe! I will maybe add some more in the future that have gone well , or PLEASE share with me your favourites too!