
Slides link <- check this out for the actucal puzzle.
One of my favourite puzzles to do in class in the frog puzzle – and it is one of those that has been done for so long, we tend to forget about it. But we should let every student experience it as it really does lend itself to the ideas of solving maths problems such as Polya’s four step outline:
- Understand The Problem
- Devise a Plan
- Carry out the Plan
- Check and Iterate
Here we understand that we have to get three frogs from one side to the other, but there are constraints. Important in my class is that I do not put the constraint on that you can’t move backwards. I like students being able to move backwards, for at least the first few minutes, as it opens up more possibilities and is a greater learning curve. It also helps make a point when we use a strategy to solve the problem.
The devise a plan stage is pretty obvious – we are going to try and move some frogs. But how, what will we use? Real frogs?! This is where we bring in some strategies, and in particular, the strategy of ACT IT OUT. I usually bring chairs to the front and get some reluctant frogs to act out the movement whilst we get help from the audience.
We could also act it out with cubes, counters, pencils, ripped up paper, whatever we can get our hands on in the resource cupboard. (there is a digital version too – I don’t like sharing this until a bit later, though sometimes it is useful for struggling students)
After a while, and the dangle of “what is the fewest moves we can do it in” I have groups exclaiming with glee that they can do it. I ask them to show me and more often than not, they get stuck or don’t do it in the moves they said they could.
(SPOILER for three frogs the answer is 15)
Oh no! I exclaim! If only we could somehow record all the steps we’ve made so we can always remember! Boom, another strategy for solving problems BE SYSTEMATIC. This is where students get creative with how they show the moves made, some go excessive with notes on whether it is a jump or a slide, some just say the colour they moved.
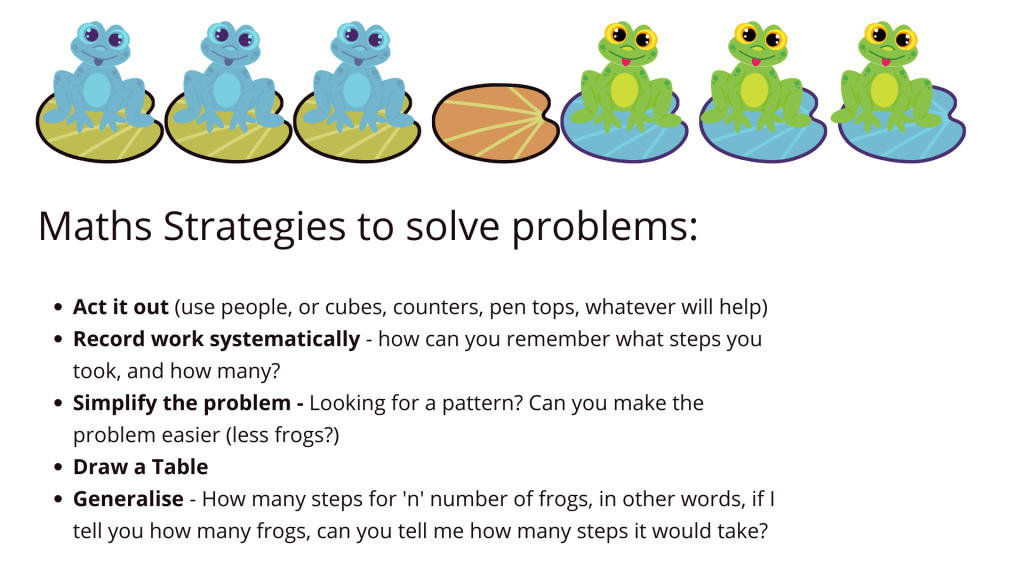
Finally we agree that 15 is the fewest moves (those that already had that, I’ve moved them onto 4 frogs). So the next step I ask is, is there a way we can ALWAYS know how many steps it will take? Baffled expressions. Okay, How about this, if I had 50 frogs on each side, how many moves would I need? Seems impossible to know, right? How about we use another maths strategy or even three: SIMPLIFY THE PROBLEM, DRAW A TABLE and also SEARCH FOR PATTERNS.
I show them a table and ask them to fill in what they know. I ask them to see any patterns. This is a bit hit and miss, sometimes a students sees something, and often they don’t. After more attempts at 4, I show them that there seems to be a multiplication link between 1 and 3, 2 and 8, and 3 and 15. At this point they predict and confirm for four frogs.
Finally we work out how many steps for 50 frogs, and also consider if we have time, what would happen in irregular cases, like frogs in circles, or 2 v 3 arrangements.
There is much more to explore with sequences and algebra – but for Y4-7 normally this is where we reach the frog limit!
